• Datariset
• Artikel
• Regresi logistik dengan minitab

Pengertian Regresi Logistik

Regresi logistik sering juga disebut model logistik atau model logit dalam ilmu statistik. Di dalam statistika regresi logistik digunakan untuk memprediksi kemungkinan (probabilitas) kejadian suatu peristiwa dengan mencocokkan data pada fungsi logit kurva logistik. Seperti analisis regresi pada umumnya, metode ini menggunakan beberapa variabel prediktor, baik numerik maupun variabel kategori. Metode ini merupakan model linier umum yang digunakan untuk regresi binomial.

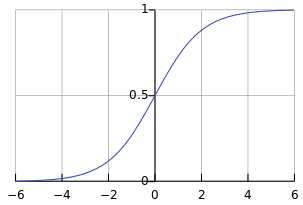
Keterangan gambar : Fungsi logistik, dengan z pada sumbu hosrizontal dan ƒ(z) pada sumbu vertikal

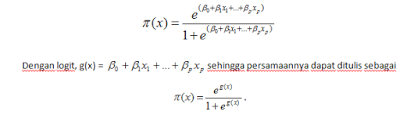
Keterangan gambar : Permodelan tentang regresi logistik

Contoh Kasus

Seorang peneliti ingin mengetahui pengaruh 10 kelompok tingkat pendapatan pertahun terhadap status keluarga sehat. Data-data yang diperoleh oleh peneliti adalah sebagai berikut :

Kelompok	Tingkat Pendapatan (satuan juta)	Jumlah Keluarga	Keluarga Sehat
1	6	40	8
2	8	50	12
3	10	60	18
4	13	80	28
5	15	100	45
6	20	70	36
7	25	65	39
8	30	50	33
9	35	40	30
10	40	25	20

Langkah pertam yang harus kita lakukan adalah. Ubah permodelan data di atas supaya bisa masuk ke dalam Minitab. Worksheet lauout dalam minitab seperti berikut :

Tingkat Pendapatan (satuan juta)	Status	Frekuensi
6	1	8
8	1	12
10	1	18
13	1	28
15	1	45
20	1	36
25	1	39
30	1	33
35	1	30
40	1	20
6	0	32
8	0	32
10	0	42
13	0	52
15	0	55
20	0	34
25	0	26
30	0	17
35	0	10
40	0	5

Keterangan Tabel :
status = 1 à sehat
status = 0 à tidak sehat
Langkah analisis dimulai dengan memilih menu Stat ⇒ Regression ⇒ Binary Logistic Regression

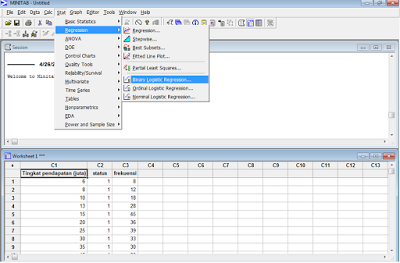
Masukkan data peubah respon yaitu status ke Response, lalu masukkan data dalam kolom frekuensi ke dalam kolom frequency. Setelah itu pada model masukkan peubah penjelas, dalam kasus ini adalah tingkat pendapatan.

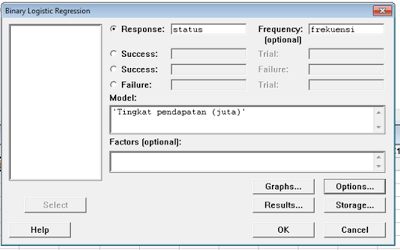
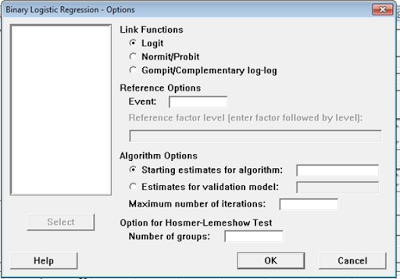
Klik pada Option ⇒ Link Function Logit ⇒ OK

Hasil Output : Binary Logistic Regression: status versus Tingkat pendapatan (juta)

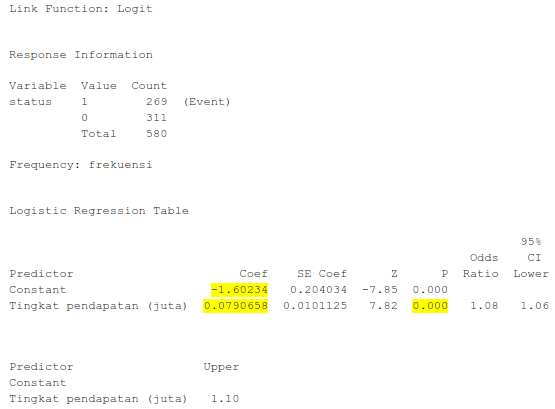
Output di atas ini sesungguhnya merupakan output untuk uji Wald (uji parsial) yang digunakan untuk menguji manakah dari perubah penjelas yang berpengaruh terhadap peubah respon. Hipotesis yang diuji adalah sebagai berikut:

• H0 : tingkat pendapatan tidak berpengaruh terhadap status
• H1 : tingkat pendapatan berpengaruh terhadap status
• Tolak H0 jika p-value < alpha (0,05)

Kesimpulan : p-value (0.00) < alpha (0.05) maka tolak H0 yang artinya cukup bukti untuk menyatakan bahwa jumlah pendapatan berpengaruh nyata terhadap status kesehatan pada taraf nyata 5%. Selain uji Wald output di atas menunjukkan koefisien regresi logistik. Sehingga persamaan regresi logistiknya adalah:

Dengan model peluang logit adalah g(x) = -1.60234+0.0791tingkat pendapatan
Log-Likelihood = -365.301
Test that all slopes are zero: G = 70.404, DF = 1, P-Value = 0.000

Uji G merupakan uji simultan yang digunakan untuk mengetahui peran seluruh peubah penjelas dalam model. Hipotesis yang diuji adalah:

• H0 : Semua peubah penjelas tidak berpengaruh terhadap status kesehatan
• H1 : minimal ada 1 peubah penjelas berpengaruh terhadap status kesehatan
• Tolak H0 jika p-value < alpha (0,05)

Kesimpulan : Pada output di atas terlihat p-value (0.000) < alpha (0.05) berarti tolak H0. Hal ini berarti bahwa minimal ada 1 peubah penjelas yang berpengaruh nyata terhadap status kesehatan pada taraf nyata 5%.

    Goodness-of-Fit Tests
    Method           Chi-Square  DF      P
    Pearson             2.34682   8  0.968
    Deviance            2.35415   8  0.968
    Hosmer-Lemeshow     2.31913   6  0.888
                        

Pengujian model logit dilakukan dengan melihat nilai statistic Goodness of fit. Metode yang sering digunakan untuk Goodness of fit data kategori adalah Pearson, Deviance dan Hosmer-Lemeshow. Hipotesis yang diuji adalah:

• H0 : model layak
• H1 : model tidak layak
• Tolak H0 jika p-value < alpha (0,05)

Kesimpulan : Dari ketiga metode yang digunakan, terlihat bahwa semua p-value nya bernilai > 0,05 sehingga terima H0 jadi dapat disimpulkan bahwa model layak.

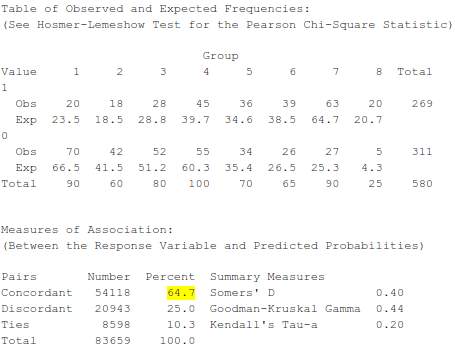
Pada bagian terakhir outputnya menjelaskan tentang keragaman peubah Y yang dapat dijelaskan oleh peubah penjelas. Untuk melihat sejauh mana keragaman peubah Y yang dapat dijelaskan oleh peubah-peubah penjelas, digunakan persen keragaman concordant. Pada kasus ini terlihat nilai percent untuk concordant 64,7%. Hal ini berarti bahwa keragaman peubah respon (status kesehatan) dapat dijelaskan oleh peubah-peubah penjelas dalam model sebesar 64,7% sedangkan sisanya dijelaskan oleh factor lain di luar model. Untuk mengetahui nilai odd ratio pada setiap kategori dapat dilakukam dengan memasukkan peubah penjelas (tingkat pendapatan) ke factors (optional) ⇒ OK.

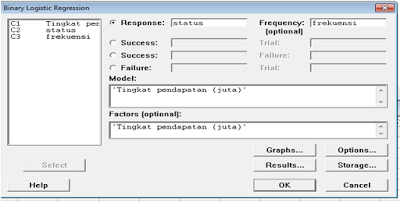
Setelah klik pada tombol sesuai gambar di atas, maka outputnya seharusnya akan nampak seperti ini :

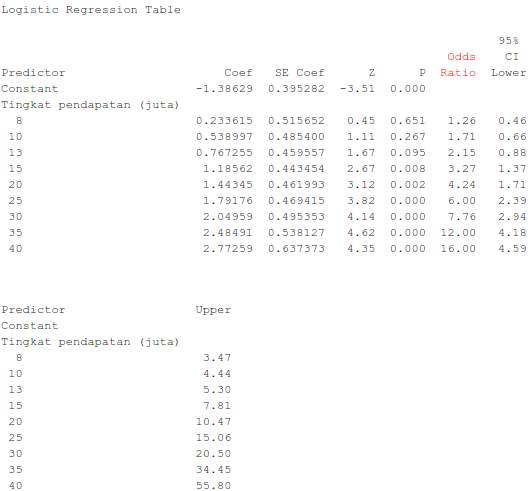
Interpretasinya :
Hasil output menunjukkan bahwa peluang penduduk dengan tingkat pendapatan 8 juta/tahun memiliki status sehat lebih besar 1,26 kali dari penduduk dengan tingkat pendapatan 6 juta/tahun, dan seterusnya. Semoga artikel ini bermanfaat bagi kita semua, jika masih ada yg dirasa kurang jelas bisa hubungi DataRiset.