Analytical Hierarchy Process
Pengertian Metode AHP, Prinsip, dan Perbandingannya
Analytical Hierarchy Process
Analytical Hierarchy Process (AHP) dikembangkan oleh Thomas L. Saaty pada tahun 1970-an. AHP merupakan sistem pembuat keputusan dengan menggunakan model matematis. AHP membantu dalam menentukan prioritas dari beberapa kriteria dengan melakukan analisa perbandingan berpasangan dari masing-masing kriteria. AHP juga merupakan suatu model yang luwes yang memberikan kesempatan bagi perorangan atau kelompok untuk membangun gagasan-gagasan dan mendefinisikan persoalan dengan cara membuat asumsi mereka masing-masing dan memperoleh pemecahan yang diinginkan darinya. Berbagai keuntungan AHP menurut Saaty (1993) adalah sebagai berikut.
- Kesatuan, yaitu AHP memberi satu model tunggal yang mudah dimengerti, luwes untuk aneka ragam persoalan terstruktur.
- Kompleksitas, yaitu AHP memadukan rancangan berdasarkan sistem dalam memecahkan persoalan kompleks.
- Saling ketergantungan, yaitu AHP dapat menangani saling ketergantungan elemen-elemen dalam suatu sistem dan tidak memaksakan pemikiran linier.
- Penyusunan hierarki, yaitu AHP mencerminkan kecenderungan alami pikiran untuk memilih elemen-elemen suatu sistem dalam tingkat yang berbeda dan mengelompokkan unsur yang serupa dalam setiap tingkat.
- Pengukuran, yaitu AHP memberi suatu skala untuk mengukur hal-hal wujud suatu metode untuk menetapkan prioritas.
- Konsistensi, yaitu AHP melacak konsistensi logis dari berbagai pertimbangan yang digunakan dalam menetapkan berbagai prioritas.
- Sintesis, yaitu AHP menuntun ke suatu taksiran menyeluruh tentang kebaikan setiap alternatif.
- Tawar menawar, yaitu AHP mempertimbangkan prioritas-prioritas relatif dari berbagai faktor sistem dan memungkinkan orang memilih alternatif terbaik berdasarkan tujuan-tujuan mereka.
- Penilaian dan consensus, yaitu AHP tak memaksakan konsensus tetapi mensintesis suatu hasil yang representatif dari berbagai penilaian yang berbeda-beda.
- Pengulangan proses, yaitu AHP memungkinkan orang memperhalus definisi mereka pada suatu persoalan dan memperbaiki pertimbangan dan pengertian mereka melalui pengulangan.
Dalam menyelesaikan persoalan dengan AHP (Saaty, 1993) ada beberapa prinsip yang harus dipahami diantaranya adalah:
a. Decompocition
Setelah permasalahan didefinisikan, maka perlu dilakukan decompocition yaitu memecah permasalahan yang utuh menjadi unsur-unsurnya. Jika ingin mendapatkan hasil yang akurat, pemecahan juga dilakukan terhadap unsur-unsurnya sampai tidak mungkin dilakukan pemecahan lebih lanjut sehingga didapatkan beberapa tingkatan dari persoalan tadi. Karena alasan ini, maka proses analisis ini dinamakan hierarki. Ada dua jenis hierarki, yaitu hierarki lengkap dan tidak lengkap. Dalam hierarki lengkap, semua elemen pada suatu tingkat memiliki semua elemen yang ada pada tingkat berikutnya, namun jika tidak, maka dinamakan hierarki tidak lengkap.
b. Comparative Judgement
Tahap ini adalah membuat penilaian tentang kepentingan relatif dua elemen pada suatu tingkat tertentu dalam kaitannya dengan tingkat di atasnya. Penilaian ini merupakan inti dari AHP, karena penilaian akan berpengaruh terhadap prioritas elemen-elemen. Hasil dari penilaian ini akan tampak lebih baik bila disajikan dalam bentuk matriks yang dinamakan matriks pairwase comparison. Pertanyaan yang biasa diajukan dalam penyusunan skala kepentingan adalah:
- elemen mana yang lebih (penting/disukai/mungkin/..) ? dan
- berapa kali lebih (penting/disukai/mungkin/..) ?
Agar diperoleh skala yang bermanfaat ketika membandingkan dua elemen, seseorang yang akan memberikan jawaban perlu pengertian menyeluruh tentang elemen-elemen yang dibandingkan dan relevansinya terhadap kriteria atau tujuan yang ingin dicapai. Dalam penilaian kepentingan relatif dua elemen berlaku aksioma reciprocal artinya jika elemen i dinilai 3 kali lebih penting dibanding j, maka elemen j harus sama dengan 1/3 kali pentingnya dibanding elemen i. Disamping itu, perbandingan dua angka yang sama akan menghasilkan angka 1, artinya sama penting. Dua elemen yang berlainan dapat saja dinilai sama penting. Jika terdapat n elemen, maka akan diperoleh matriks pairwise comparison berukuran n x n.
c. Synthesis of Priority
Setiap matriks pairwise comparison kemudian dicari eigen vector untuk mendapatkan local priority, karena matriks pairwise comparison terdapat pada setiap tingkat, maka untuk mendapatkan global priority harus dilakukan sintesa di antara local priority. Prosedur melakukan sintesa berbeda menurut bentuk hierarki. Pengurutan elemen-elemen menurut kepentingan relatif melalui prosedur sintesa dinamakan priority setting.
d. Logical Consistency
Logical consistency menyatakan ukuran tentang konsisten tidaknya suatu penilaian atau pembobotan perbandingan berpasangan. Pengujian ini diperlukan, karena pada keadaan yang sebenarnya akan terjadi beberapa penyimpangan dari hubungan tersebut sehingga matriks tersebut tidak konsisten sempurna. Hal ini dapat terjadi karena ketidak konsistenan dalam preferensi seseorang.
Hierarki adalah alat yang paling mudah untuk memahami masalah yang kompleks di mana masalah tersebut diuraikan ke dalam elemen-elemen yang bersangkutan, menyusun elemen-elemen tersebut secara hierarkis dan akhirnya melakukan penilaian atas elemen-elemen tersebut sekaligus menentukan keputusan mana yang akan diambil. Proses penyusunan elemen-elemen secara hierarki meliputi pengelompokan elemen-elemen dalam komponen yang sifatnya homogen dan menyusun komponen-komponen tersebut dalam level hierarki yang tepat. Hierarki juga merupakan sistem yang tingkatan-tingkatan keputusannya bertingkat dengan beberapa elemen keputusan pada setiap tingkatan keputusan. Secara umum, hierarki dapat dibagi dua jenis (Permadi, 1992) yaitu:
- Hierarki struktural, yang berfungsi menguraikan masalah yang kompleks diuraikan menjadi bagian-bagiannya atau elemen-elemennya menurut ciri atau besaran tententu sepenti jumlah, bentuk, ukuran, atau warna, dan
- Hierarki fungsional, menguraikan masalah yang kompleks menjadi bagian yang sesuai hubungan esensialnya.
Penyusunan hierarki dilakukan untuk menggambarkan elemen sistem atau alternatif keputusan yang teridentifikasi. Abstraksi susunan hierarki keputusan dapat dilihat dibawah ini:
- level 1: fokus/sasaran utama
- level 2: faktor/kriteria
- level 3: sub-factor
- level 4: obyektif
- level 5: alternatif
Setiap hierarki tidak perlu selalu terdiri dari 5 level, banyaknya level tergantung pada permasalahan yang sedang dihadapi. Tetapi untuk setiap permasahan, level 1 (fokus/sasaran), level 2 (faktor/kriteria), dan level 5 (alternatif) harus selalu ada. Contoh model struktur AHP 4 level dengan n kriteria dan m alternatif dapat dilihat pada Gambar 3.1 berikut.
Tiap tingkatan dan hieraki keputusan mempengaruhi faktor puncak atau tujuan utama dengan intensitas yang berbeda. Melalui penerapan teori matematika pada hierarki dapat dikembangkan suatu metode yang mengevaluasikan dampak dari suatu tingkat keputusan terdekat diatasnya, yaitu berdasarkan komposisi kontribusi relatif (prioritas) dan tiap elemen pada tingkat keputusan terhadap setiap elemen dan tingkat keputusan terdekat.
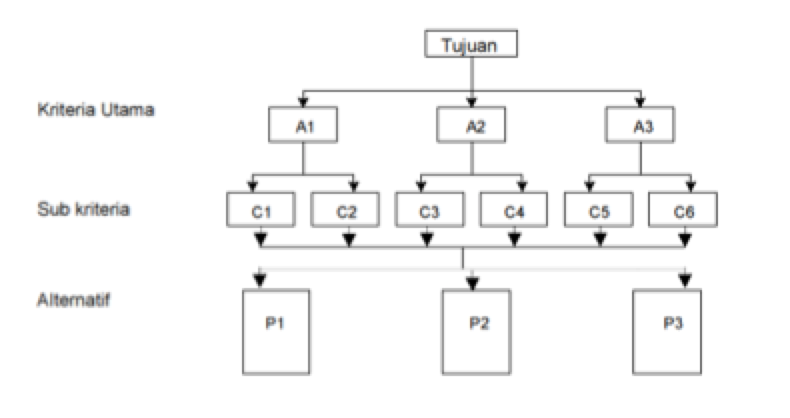
Gambar : Model Struktur AHP 4 Level
Dalam pengambilan keputusan hal yang perlu diperhatikan adalah pada saat pengambilan data, di mana data ini diharapkan dapat mendekati nilai yang sesungguhnya, misalnya, derajat kepentingan konsumen dapat dilakukan dengan pendekatan perbandingan berpasangan. Perbandingan berpasangan sering digunakan untuk menentukan kepentingan relatif dari elemen-elemen dan kriteria-kriteria yang ada. Perbandingan berpasangan tersebut diulang untuk semua elemen dalam tiap tingkat. Elemen dengan bobot paling tinggi adalah pilihan keputusan yang layak dipertimbangkan untuk diambil. Untuk setiap kriteria dan alternatif, kita harus melakukan perbandingan berpasangan (pairwise comparison), yaitu membandingkan setiap elemen dengan elemen yang lainnya pada setiap tingkat hierarki secara berpasangan sehingga didapat nilai tingkat kepentingan elemen dalam bentuk pendapat kualitatif.
Untuk mengkuantifikasi pendapat kualitatif tersebut digunakan skala penilaian sehingga akan diperoleh nilai pendapat dalam bentuk angka. Menurut Saaty (1990), untuk berbagai permasalahan, skala 1 sampai 9 merupakan skala yang terbaik dalam mengkualifikasikan pendapat, yaitu berdasarkan akurasinya berdasarkan nilai Root Mean Square (RMS) dan Median Absolute Deviation (MAD). Nilai dan definisi pendapat kualitatif dalam skala perbandingan Saaty ada pada Tabel di bawah ini :
Skala Matrik Perbandingan Berpasangan
| Intensitas Kepentingan | Definisi | Penjelasan |
| 1 | Elemen yang satu sama pentingnya dibanding dengan elemen yang lain (equal importance) | Kedua elemen menyumbang sama besar pada sifat tersebut |
| 3 | Elemen yang satu sedikit lebih penting dari pada elemen yang lain (moderate more importance) | Pengalaman menyatakan sedikit memihak pada satu elemen |
| 4 | Elemen yang satu jelas lebih penting dari pada elemen yang lain (essential, strong more importance) | Pengalaman menunjukkan secara kuat memihak pada satu elemen |
| 7 | Elemen yang satu sangat jelas lebih penting dari pada elemen yang lain (demonstrated importance) | Pengalaman menunjukkan secara kuat disukai dan didominasi oleh sebuah elemen tampak dalam |
| 9 | Elemen yang satu mutlak lebih penting dari pada elemen yang lain (absolutely more importance) | Pengalaman menunjukkan satu elemen sangat jelas lebih penting |
| 2,4,6,8 | Apabila ragu-ragu antara dua nilai yang berdekatan (grey area) | Nilai ini diberikan bila diperlukan kompromi |
| 1/(2-9) | Jika kriteria C1 mendapatkan satu angka bila dibandingkan dengan kriteria C2 memiliki nilai kebalikan bila dibandingkan C1 | Jika kriteria C1 mempunyai nilai x bila dibandingkan dengan kriteria C2, maka kriteria C2 mendapatkan |
Nilai-nilai perbandingan kriteria yang telah didapatkan, kemudian diolah untuk menentukan peringkat kriteria dari seluruh kriteria yang ada, baik kriteria kualitatif maupun kriteria kuantitatif dapat dibandingkan sesuai dengan judgment yang telah ditentukan untuk menghasilkan bobot dan prioritas.

 Artikel
Artikel
- Analytical Hierarchy Process
- Aplikasi untuk Olah Data Statistik
- Belajar SPSS
- Cross Tabulasi
- Data Envelopment Analysis
- Estimasi dalam Regresi Linear
- Jasa Olah Data Skripsi, Tesis, dan Penelitian di Jakarta
- Microsoft Excell untuk Olah Data
- Model Persamaan Struktural
- Model Probit
- Olah Data Menggunakan EViews
- Penelitian dan Data
- Penelitian Kualitatif dan Kuantitatif
- Penelitian Murni dan Penelitian Semu
- Permasalahan dalam Olah Data
- Persamaan Model Regresi Linear
- Prosedur Pemilihan Model dalam Regresi
- Regresi Logistik menggunakan Minitab
- Sejarah Model Persamaan Struktural
- Statistik Parametric dan Non Parametric
- Uji Anova Dua Faktor
- Uji Coba Instrument, Uji Validitas, Try Out
- Uji Mantel Haenszel
 Tahukah Kamu?
Tahukah Kamu?